Building Math Fact Fluency: Near Doubles Subtraction Strategy
Help your students build their math fact fluency by teaching the near doubles subtraction strategy. (This strategy may also be called using doubles.) Once the students have learned the strategy, they can build their math fact fluency by playing games to practice the strategies.
Memorization of facts does not work for all students. They need explicit instruction on learning the strategies.
Since you want all of your students to be successful, you need to explicitly teach the strategies.
But wait... How do you teach the near doubles subtraction strategy?
Have you taught the near doubles addition strategy first? If not, go do that NOW!
Since subtraction and addition are related, it’s helpful to teach the addition strategy first.
The near doubles strategy is harder for students to understand than the addition strategy. But that doesn’t mean it won’t work for them!
There isn’t a “trick” or a fast shortcut for teaching the near doubles subtraction strategy. You have to think of addition in order to use this strategy. It’s important for students to understand that addition and subtraction are related. So get to reviewing fact families if your students are still struggling with this.
Relating Addition and Subtraction

Let’s look at this example:
15 – 8
The students know to think of 8 + ___ = 15. (See why the students NEED to know their addition facts?)
The students who know their addition facts will be able to quickly get the answer: 7.
So 15 – 8 = 7.
But that only relates addition and subtraction. What about the strategy?

Near Doubles Subtraction Strategy
This way can be confusing, but it does work. Let’s use the same example problem.
- Look at the problem and determine if it is a near doubles problem. To do this, double the second number in the problem.
- Example: 15 – 8 = _____.
- Double the 8, which is 8 + 8 = 16.
- Since the answer 16 is one away from the 15 in the original problem, the near doubles strategy can be used.
- You’ve already doubled 8, so you’ll use that for the next step.
- 15 is one less than 16, so you have to take one away from one of the 8s.
- Then you get 8 + 7 = 15.
- In this case, when you doubled, the sum was greater than the sum in the original problem, so you have to take away one.
- In other cases, the sum when you double the addend is less than the addend in the original problem, so you would add one to an addend.
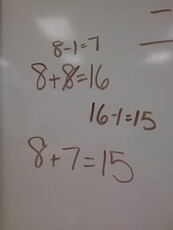
Important Note:
I wrote out the steps on the board to show the students my thinking while using the near doubles subtraction strategy.
Since you are trying to build math fact fluency, all of this work should be done mentally. Students can show this thinking when they are just starting to learn the strategy, but they should work up to doing all the thinking in their heads.


Building Math Fact Fluency with Games
Students love to play games and don’t even realize they are learning! You can use any of these games to practice the near doubles strategy.
These games are very low prep. Print, copy, find materials (dice, counters, pencils), and PLAY!
There are many ways you can use math fact games for your students:
- Early finishers
- Small Group
- Whole Class
- Homework
- Substitute Plans





